イラストレーターと
ハンドメイド作家の
理学療法士のサイト

■膝は確かに楽。でも股関節は…？

　前回のコラムでは、階段を昇り降りするときには上半身を前傾させた方が膝が楽になるという話をし、そして最後には本当は楽になっていない、などと含みを持たせた終わり方をしました。今回はその解説をします。
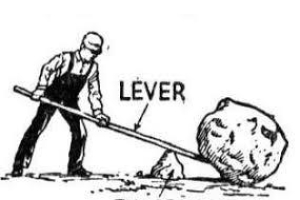
　前傾姿勢になると膝が楽になる理由を、テコの原理を用いて説明しましたが、テコと聞いてイメージするのはこのイラストのような場面ではないでしょうか。テコを使うと、少ない力でも重い岩を動かすことができますが、そのかわり直接岩を持ち上げるよりも長い距離を動かさなければなりません。理科でいう“仕事”とは力×距離なので、直接岩を持ち上げても、テコを使って少ない力で持ち上げても、同じ仕事をしていることになります。力か距離か、どちらで楽をするかの違いです。
　全く同じではありませんが、似たようなことが階段の昇り降りでも起きていると考えてください。前回のコラムで膝が楽になる方法について解説しましたが、膝が楽になる代わりに、実はそのぶん他の場所での負担が増えているのです。その場所とは、股関節です。


■膝とお尻、どっちかが疲れる

　上半身を起こして階段を昇り降りするとき、上半身の重みは股関節にかかっています。重みのかかる場所が膝から遠いので、膝の負担が大きくなるのは前回の解説の通りです。そして股関節はというと、直上に身体が乗っているだけなので、バランスがとれていれば股関節の筋肉はあまり使っていません。もちろん姿勢が崩れないよう最低限の力は入っていますが、あまり意識することは無いでしょう。
　それに対し前傾姿勢ではどうかというと、上半身の重みのかかる場所が膝に近くなるため、膝の負担は小さくなります。しかしそのかわり、前に倒れそうになる上半身を支える必要が出てきてしまいます。これを支えるのは股関節にある“大殿筋”という筋肉です。上半身が前に倒れないよう、大殿筋で常に支え続ける必要がありますので、前傾姿勢で階段を昇り降りしていると、膝が疲れない代わりにお尻が疲れてきます。


■疲れる場所を操作するという戦略

　「なんだ結局一緒かい！」と思った方。そうです。結局一緒です。どこが一番疲れるかが違うだけで、疲れるのは一緒なんです。しかし私はこの“どこが一番疲れるかを意図的に操作できる”ということが非常に重要であると考えます。
　病院には様々な痛みを抱えた人が訪れ、私は理学療法士として動作のアドバイスをします。膝が痛い人は前傾姿勢で階段の昇り降りをすればいいですし、股関節が痛い人は上半身を起こせばいいのです。意図的に負担がかかる場所を変えることができるのは大きなメリットです。
　また私たちが趣味で山登りをしたり、長い階段を昇り降りしなければならないとき、途中で「膝が疲れてきたな」と感じたら、少し前傾姿勢になれば膝の負担をお尻に逃がすことができます。そして膝の疲れが癒えてきたころ姿勢を元に戻せば、今度はお尻が楽になります。

　このコラムを書いていて思い出したのですが、小学生のとき、遠足の山登りで皆が疲れてきたころ「後ろ向きで進むと疲れないぞ！大発見！」などと言い出す子がクラスに必ず一人はいました。それを聞いて皆も試してみて、“本当だ大発見派”と“そんなの気のせい派”に分かれたものです。私は今回のお話をふまえて、“本当だ大発見派”の主張は運動学的に非常に理に適ったものであると考えます。
　しかし“そんなの気のせい派”の意見も否定できないのです。きっとその子らは、もともと少し前傾姿勢で登っていたのでしょう。だから後ろ向きになって前傾姿勢になったとしても、その変化を感じられないのです。子供の頃の何気ない思い出も、真面目に分析してみると意外な発見があるのだなあ、と驚くとともに、少し懐かしく感じました。


■もっと詳しく！（リハビリ専門職向け）

　上半身を前傾させることで膝の負担はどれくらい減るのか。計算で求めることができますから、もう少し踏み込んでみましょう。
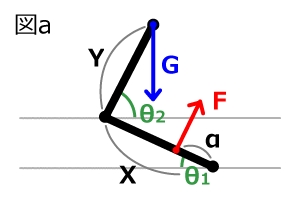
　まず、上半身の重さをGとします。膝から股関節までの距離をXとし、股関節から上半身の重心までの距離をYとします。上半身の重心は第7〜9胸椎にあり、第9胸椎はちょうど剣状突起のあたりですから、外から計測することができます。そして膝から大腿四頭筋の付着部までの距離をαとします。大腿骨の水平からの角度をθ1、上半身の水平からの角度をθ2とします（図a）。
　
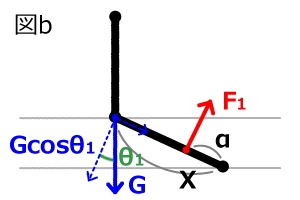
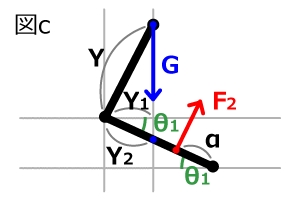
　はじめに上半身が直立している場合（図b）ですが、このときに要求される大腿四頭筋の筋力をF1とすると、膝関節伸展方向のモーメントはF1αとなり、それに対し屈曲モーメントはGcosθ1Xとなります。次に上半身が傾斜している場合。こちらはちょっとややこしいのですが、重心線が大腿骨のどのあたりを通っているかを求めます。図cにおいて、Y1はYcosθ2で表せます。そしてY1＝Y2 cosθ1も成り立つことからYcosθ2＝Y2 cosθ1となり、Y2＝Ycosθ2/ cosθ1となります。重心線が通っている場所はXからY2を引いた位置ですので、X- Ycosθ2/ cosθ1になります。あとは直立のときと同じ方法で、伸展モーメントはF2α、屈曲モーメントはGcosθ1(X- Ycosθ2/ cosθ1)と表せます。
　それぞれの姿勢で伸展モーメントと屈曲モーメントは釣り合っていますので、

　　　F1α＝Gcosθ1X
　　　F2α＝Gcosθ1(X- Ycosθ2/ cosθ1)

　が成り立ちます。両辺をαで割って”F＝”の形になおすと、

　　　F1＝Gcosθ1X/α
　　　F2＝Gconθ1(X-Ycosθ2/cosθ1)/α

　となります。両者を比で表し、F1とF2に上記の値を代入すると、

　　　F1：F2＝Gcosθ1X/α：Gconθ1(X-Ycosθ2/cosθ1)/α

　となり、両辺をGconθ1/αで割って、

　　　F1：F2＝X：X-Ycosθ2/cosθ1

　となります。ここから先は代数の実測です。写真の職員で測ってみると、20cm台の昇降をするとき、Xは45cm、Yは33cm、θ1は50°、θ2は62°でした。cos50°は0.64、cos62°は0.47ですから、計算すると

　　　F1：F2＝45：20.91
　　　≒15：7

　となりました。写真の職員と同じくらい上半身を傾けた場合、膝を伸ばすための筋力は上半身が直立している場合と比べて実に半分以下で済むことになります。これは大きな違いですね。
体格や段の高さによって計算値に違いが出てくるはずですが、理論上は上半身を倒せば倒すほど膝は楽になります。ただしその楽になった分の負担は大殿筋にかかってきますし、上半身を倒すほどにその姿勢を維持するための体幹筋の負荷も増えてきますからほどほどに。